코테: 금과 은 운반하기

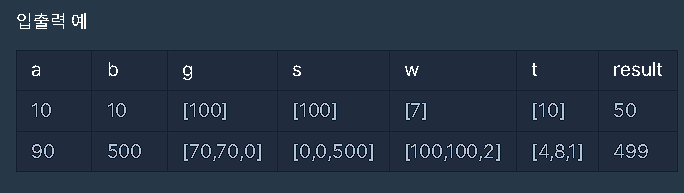
다시 한번 조건을 정리해보자: a: 필요한 금의 무게 b: 필요한 은의 무게 새로운 도시의 수= 배열 요소의 개수 g: 배열당 운반 가능한 금의 무게 s: 배열당 운반 가능한 은의 무게 w: 최대 운반 가능한 무게 t: 각각의 도시마다 편도로 운반 가능한 시간 이 정보들을 토대로 a kg의 금, b kg의 은을 운반하는 최적의 시간을 result로 반환해야 한다.

이 조건들 아래에서는 운반 트럭이 왕복 그 이상의 거리를 운행해야 한다. 조건 1: 금의 무게 g가 최대 무게 w를 넘길 때? 조건 2: 은의 무게 s가 최대 무게 w를 넘길 때? 조건 3: 광물 각각은 편도로 옮길 수 있으나, 금 + 은의 (g+s) 무게가 최대 무게 w를 넘길 때? 이때에 한하여, t는 추가로 계산해야 한다는 뜻이다.

그리고 해당 t는 각 도시마다 걸리는 편도의 시간이기에, 모든 주어진 도시 (배열 요소당) t를 구해서 합해줘야 최적의 운반 시간을 구할 수 있다.

해당 문제는 이진 탐색을(Binary Search) 적용해야 최적값을 구하기 쉽다.

최소값 0을 left, 제한 사항 중 가장 큰 값인 1e9(10^9) 보다 높은 임의의 숫자를 right로 놓고 풀자. 참고로 이 문제의 최종 값은 매우 크므로 long long 자료형 변환을 잊지말자.

추가로 사용한 변수는 이진 탐색의 진행에 따라 합산해야 하는 값들이다. 현재 총 금의 무게 g의 합 totalGold, 현재 총 은의 무게 s의 합totalSilver, 현재 모든 광물의 무게 w의 합 totalWeight, 현재 운반에 걸린 편도 횟수trips,모든 편도 횟수 trips로 계산된 무게 w들의 현재 합 maxTransport

// 탐색 시작
while (left <= right) {
        long long mid = (left + right) / 2; //반으로 탐색 조건 줄이기
        long long totalGold = 0, totalSilver = 0, totalWeight = 0;

        for (int i = 0; i < g.size(); i++) {
            long long trips = mid / (2 * t[i]);  // 왕복 가능 횟수
            if (mid % (2 * t[i]) >= t[i]) trips++;  // 편도 운반 가능하면 추가

            long long maxTransport = trips * w[i]; // 이 도시의 최대 운반량
            totalGold += min((long long)g[i], maxTransport);  // long long로 타입 맞추기
            totalSilver += min((long long)s[i], maxTransport);  // long long로 타입 맞추기
            totalWeight += min((long long)(g[i] + s[i]), maxTransport);  // long long로 타입 맞추기
        }

        if (totalGold >= a && totalSilver >= b && totalWeight >= a + b) {
            answer = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

문제의 조건을 잘못 이해하고, 최대 가능 시간을 주어진 가장 큰 값이었던 1e9의 시간을 right로 설정해서 오답이 발생했었다. 1e15로 테스트해보니 모든 케이스를 통과했다.